Grundlagen der anwendungsbezogenen Hochschulmathematik
2. Folgen und Grenzwerte
2.3. Elementare Eigenschaften von Folgen

In diesem Abschnitt werden grundlegende Eigenschaften von Folgen dargelegt.

Endliche und unendliche Folgen
Wie bereits erwähnt sind der Definitionsbereich einer Folge die natürlichen Zahlen \(\mathbb{N}\). Daher ist der Definitionsbereich (abzählbar) unendlich. Man kann aber theoretisch auch nur eine (endliche) Teilmenge der natürlichen Zahlen als Definitionsmenge nutzen. Im Weiteren werden wir aber immer ganz \( \mathbb{N} \) als Definitionsmenge verwenden und uns strikt an die Definition aus 2.1 halten.
Wir betrachten kurz die nachfolgenden Beispiele:
Beispiel 1.
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) | \(a_{6}\) |
| -1 | 1 | -1 | 1 | -1 | 1 |
Dies ist eine Folge, die aus sechs Folgengliedern besteht und die alternierende Folge \((\pm 1)^n\) repräsentiert. Ihre Definitionsmenge ist eine endliche Teilmenge der natürlichen Zahlen. Daher heißt, die Folge \(\left( a_n \right)\) endlich.
Beispiel 2.
| \(b_{n}\) | \(b_{1}\) | \(b_{2}\) | \(b_{3}\) | \(b_{4}\) | \(\ldots\) | \(b_{n}\) | \(\ldots\) |
| -1 | 1 | -1 | 1 | \(\ldots\) | \(\left( -1 \right)^{n}\) | \(\ldots\) |
Obwohl die Folge ähnlich zu der Folge im Beispiel 1 ist, ist die Folge unendlich. Ihr Definitionsbereich ist nicht beschränkt und ist für jede natürliche Zahl definiert.
Steigende und fallende Folgen
Definition 1
Eine Folge \(\left( a_n \right)\) heißt monoton steigend, falls jedes nachfolgende Folgenglied größer oder gleich dem vorhergehenden Folgenglied ist, d.h. es gilt \(a_{n+1} \geq a_n\) für alle \(n\) aus dem Definitionsbereich der Folge.
Beispiel 3.
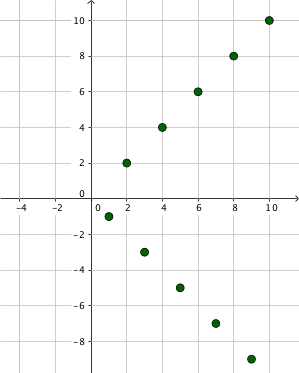
Betrachte die Fibonacci-Folge (hier abgekürzt mit \( (c_n) \)
|
\(c_{n}\) |
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) |
| \(1\) | \(1\) | \(2\) | \(3\) | \(5\) | \(\ldots\) |
|
\(d_{n}\) |
\(d_{1}\) | \(d_{2}\) | \(d_{3}\) | \(d_{4}\) | \(d_{5}\) | \(d_{6}\) |
| \(-1\) | \(-\frac{1}{2}\) | \(-\frac{1}{3}\) | \(-\frac{1}{4}\) | \(-\frac{1}{5}\) | \(\ldots\) |
Fibonacci-Folge
Bemerkung: Die konstante Folge\(\left( 1,~ 1,~ 1,~ 1,~ 1,~ ... \right)\) ist sowohl monoton steigend als auch monoton fallend, da u.a. die Ungleichung aus Definition 1 erfüllt ist.
Um die Wiederholung von Folgengliedern zu vermeiden, wird folgender Begriff eingeführt:
Definition 2
Eine Folge \(\left( a_n \right)\) heißt streng monoton steigend, falls \(a_{n+1} > a_n\) für alle \(n\) gilt.
Monoton fallende und streng monoton fallende werden analog definiert.


Beschränkte Folgen
Um die Eigenschaften von beschränkten und unbeschränkten Folgen zu beschreiben, müssen wir nicht den Definitionsbereich, sondern den Wertebereich betrachten.
Falls eine Zahl \(M\) existiert, so dass \(a_n \leq M\) für alle \(n\) gilt, so heißt die Folge \(\left( a_n \right)\) von oben beschränkt und die Zahl \(M\) heißt obere Schranke. Analog bedeutet die Existenz einer Zahl \(N\) mit \(a_n \geq N\) für alle \(n\), dass die Folge \(\left( a_n \right)\) nach unten beschränkt ist und die Zahl \(N\) ist eine untere Schranke.#
Zusatzfrage:
Sind die Folgen der Beispiele 4.-6. monoton wachsend oder fallen?
Beispiel 4.
Die Folge der Primzahlen \(\left( 2,3,5,7,11, ... \right)\) ist eine unendliche Folge, da es unendlich viele Primzahlen gibt, und unbeschränkt, da zusätzlich jede dieser größer ist als ihr Vorgänger.
Beispiel 5.
Die Folge der ganzen Zahlen \(\left( -1,- 2,- 3,- 4,- 5, ... \right)\) ist beispielsweise nach oben beschränkt durch die Zahl \(0\), aber nicht nach unten, da jede mögliche Schranke nach unten unterschritten wird.Die Folge der geraden Zahlen \( \left( 2, 4, 6, 8, ... \right) \) ist analog nach unten durch \( 0 \), aber auch durch \( 1 \) beschränkt.
Beispiel 6.
Die Folge \(\left( -1,~ 2,~ -3,~ 4,~ -5, ..., (-1)^n \cdot n, ... \right)\) ist weder nach oben noch nach unten beschränkt. Wir können sowohl beliebig große als auch beliebig kleine Folgenglieder wählen, die größer bzw. kleiner als jede denkbare Schranke sind.

Konvergente und divergente Folgen
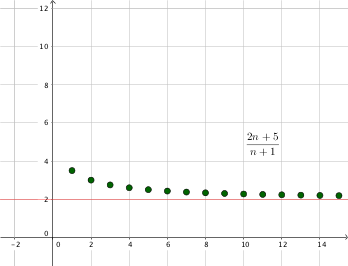
Konvergenz ist eine sehr wichtige Eigenschaft von Folgen. Wenn eine Folge konvergiert, so nähern sich die Folgenglieder einen bestimmten Wert beliebig nahe an (oder erreichen ihne). Diesen nennt man den Grenzwert der Folge (dass er existiert, wird später noch gezeigt). Beispielsweise illustriert der Graph auf der rechten Seite, dass die Folge \(a_n = \frac{2n+5}{n+1}\) gegen den Wert \(2\) konvergiert. Hierbei weichen ab einen bestimmten Index die Folgenglieder um weniger als einen beliebig kleinen, frei wählbaren Wert von \(2\) ab.
Definition 3 (konvergente Folge)
Es sei \( \left( a_n \right)\) eine Folge von reellen Zahlen. Diese heißt konvergent,
falls es eine reelle Zahl \(a\) gibt, so dass zu jeder Zahl \(\epsilon > 0\) ein \(N_{\epsilon}\) existiert mit \(\vert{ a_n - N_{\epsilon}}\vert< \epsilon\) für alle \(n \rightarrow N_{\epsilon}\). Man sagt dann, dass \(\left( a_n \right)\) gegen \(a\) konvergiert und nennt die Zahl \(a\) den
Grenzwert oder den Limes der Folge, und man schreibt
\( a= \lim\limits_{n \to \infty} a_n \)
oder
\( \left( a_n \right) \rightarrow a\) für \( n \rightarrow \infty \)
Wenn eine Folge nicht konvergent ist, dann heißt sie divergent.

Ein sehr banales Beispiel liefert die konstante Folge \(\left( 1,1,1,1, ... \right)\), die gegen \( 1 \) konvergiert. Hier stimmen Grenzwert und Wert des Folgenglieds in jedem Eintrag sogar überein. Als \( N_{epsilon} \) kann somit jedes beliebige \( N \in \mathbb{N} \) gewählt werden.
Um die Definition zu verstehen, wollen wir uns zunächst ein einfacheres Beispiel betrachten. Wir wählen hierfür \( (a_n)=\frac1n \). Die Vermutung liegt nahe, dass \( (a_n) \) gegen \(0\) konvergiert. Konvergenz kann man sich dabei so vorstellen, als ob ein Gegenspieler eine beliebig kleine positive Zahl \( \epsilon \) nennt und wir versuchen einen Index \( N_{\epsilon} \) zu finden, sodass alle folgenden Folgenglieder (\( a_n \) mit \( n \geq N_{\epsilon} \)) um weniger als \( \epsilon \) vom Grenzwert abweichen. Wir wollen dies nun für \( (a_n) \) zeigen, wie so etwas aussehen kann.

Dabei haben wir ausgenutzt, dass \( \frac1n \) stets größer-gleich 0 ist und haben \( N_{\epsilon} > \frac{1}{\epsilon} \) nach \( \epsilon \) umgeformt. Dabei fällt das entsprechende \( N_{\epsilon} \) meist vom Himmel. In diesem Beispiel war das noch gut nachvollziehbar, aber wir wollen ein weiteres Beispiel betrachten, wo dies nicht so einfach der Fall ist.
Beispiel:
Es kann bewiesen werden, dass die Folge \(a_n = \frac{2n+5}{n+1}\) aus dem Einstieg gegen \(2\) konvergiert. Dazu ziehen wir den Bruch zunächst auseinander:
\[\frac{2n+5}{n+1} = 2 + \frac{3}{n+1},\]
wobei der Summand \(\frac{3}{n+1}\) für hinreichend großes \(n\) beliebig klein wird.

Wichtig: Diese Überlegungen wollen wir aber nicht bei jeder Grenzwertbetrachtungen durchführen, da sie doch etwas aufwändiger sind. Hat man eine Folge in der in Zähler und Nenner ein Polynom (z.B. mit Variablen \( n\)) stehen, so lässt sich mit der Definition der Konvergenz zeigen:
- Ist Zählergrad < Nennergrad, dann konvergiert die Folge gegen 0
- Ist Zählergrad = Nennergrad, dann konvergiert die Folge gegen den Quotienten der Leitkoeffizienten
- Ist Zählergrad > Nennergrad, dann divergiert die Folge gegen \( +\infty \) oder \( -\infty \), je nach Vorzeichen des Leitkoeffizienten des Zählerpolynoms
Im Beispiel \( \frac1n \) ist der Zählergrad gleich 0 ("konstantes Polynom") und der Nennergrad gleich 1. Im zweiten Beispiel sind beide Grade gleich 1; der Quotient ist dann \( \frac21 = 2 \).
Ein Beispiel für eine Folge, die kein Quotient zweier Polynome ist, aber dennoch gegen \( +\infty \) divergiert, liefert die Primzahlenfolge aus Beispiel 6.

Lemma
Jede konvergente Folge ist beschränkt.

Bemerkung: Die umgekehrte Aussage, dass jede beschränkte Folge konvergent ist, ist nicht richtig. Wir betrachten hierzu die Folge \(b_n=\left( 1,~ -1,~~ 1,~ -1,~ ... \right)\): Die Folge ist beschränkt mit Schranken \(-1\) und \(1\), aber sie konvergiert nicht:
Würde sie konvergieren, so gäbe es einen Grenzwert \(A\) und für jedes \( \epsilon \) ein \( N_{\epsilon} \, (\textrm{manchmal auch} \, n_0) \in \mathbb{N} \) geben, so dass für alle \(n>n_0\) gilt: \(|b_n - A| < \epsilon\) gilt. Insbesondere auch für \( \epsilon=0,5 \). Dann könnten wir nie ein solches \(A\) und \( n_0 \) finden: Da zwischen \(1\) und \(-1\) der Abstand \(2\) liegt und wir beide unendlich oft wieder als nachfolgende Folgenglieder erhalten, können wir wegen \( \epsilon = 0,5 \) keinen Grenzwert \( A \) haben.
Beispiel 7.
Hat die Folge \((a_n)\) definiert durch \[a_n=1+(-1)^n\cdot\frac1n\] für \(n\in\mathbb{N}\) eine obere Schranke?
Wegen \[\vert(-1)^n\cdot\frac1n\vert\leq1\] für \(n\in\mathbb{N}\) ist \(2\) eine obere Schranke für die Folge. Aber es ist auch \(a_2=\frac32\) oder \(3\) eine obere Schranke für die Folge. Beachte, dass die obere und untere Schranke einer Folge nicht eindeutig ist. Eindeutig ist nur die kleinste obere und die größte untere Schranke einer Folge. In diesem Fall ist die kleinste obere Schranke \(a_2=\frac32\); eine kleinste obere bzw. größte untere Schranke muss aber kein Folgenglied sein wie die Folge \(\frac1n\) zeigt, da hier \(0\) die größte untere Schranke ist.
Beispiel 8.
Ist die Folge \[a_n=\frac{4n-4}{2n-1}\] für \(n\in\mathbb{N}\) monoton steigend oder monoton fallend? Bestimme ihren Grenzwert für \(n\to\infty\) sofern existent.
Wir haben \[a_n=2-\frac{2}{2n-1}.\] Daher ist die Folge monoton steigend, weil die Folge \((-\frac{2}{2n-1})\) monoton steigend ist. Statt dem Epsilon-Kriterium aus der Definition können wir daher auch das Verhalten für \(n\) gegen \( \infty\) untersuchen:
Da \((-\frac{2}{2n-1})\) für \(n\to\infty\) gegen \(0\) strebt (Nenner wird beliebig groß und Zähler ist konstant; der Bruch wird deshalb beliebig klein), ist der Grenzwert \(2\).
Beispiel 9.
Ist die Folge \[a_n=\frac{4n^2+n+4}{n^2+1}\] für \(n\in\mathbb{N}\) monoton steigend oder monoton fallend? Bestimme ihren Grenzwert für \(n\to\infty\) sofern existent.
Wir haben \[a_n=4+\frac{n}{n^2+1}.\] Die Folge ist monoton fallend , weil \((\frac{n}{n^2+1})\) monoton fallend ist. Der Grund hierfür ist, dass Nenner für \[n\in\mathbb{N}\] viel schneller wächst als der Zähler.
Da \((\frac{n}{n^2+1})\) für \(n\to\infty\) gegen \(0\) strebt, ist der Grenzwert \(4\).

Übung 2.
Es sei \[a_n=\frac{6n-2}{2n+2}\] für \(n\in \mathbb{N}\). Finde das kleinste \(n_0\), so dass \[\vert a_n-3\vert<\epsilon\] mit \(\epsilon =\frac{1}{100}\) für alle \(n\geq n_0\) gilt.

Übung 3.
Es sei \[a_n=\sqrt{n+1}-\sqrt{n}\] für \(n\in\mathbb{N}\). Finde den Grenzwert der Folge \((a_n)\).

Übung 4.
Finde für die Folge \( \left( f_n \right) = \left( \sqrt{3} \cdot 2^{1-n} \right) \) den Index \( n \), ab dem alle Folgenglieder kleiner als \( \frac{1}{512} \) sind.