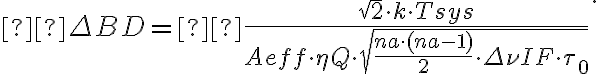Lecture - Fundamental Concepts
4. Receiver Response
4.2. Interferometer sensitivity
In order to estimate whether a source can be detected by a radio telescope or array, the so-called signal-to-noise ratio (SNR) has to be calculated. For a single telescope the signal is given by the measured antenna temperature 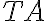 and the noise is given by the radiometer equation
and the noise is given by the radiometer equation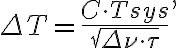
in which 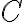 is a dimensionless constant depending on the receiver system used,
is a dimensionless constant depending on the receiver system used, 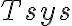 is the system temperature,
is the system temperature, 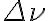 is the bandwidth of the receiver equipment and
is the bandwidth of the receiver equipment and 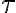 is the integration time.
is the integration time.
In radio interferometry, the signal is given by the brightness distribution 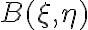 of a source that must be calculated by the Fourier integral of the measured visibility
of a source that must be calculated by the Fourier integral of the measured visibility 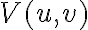 :
: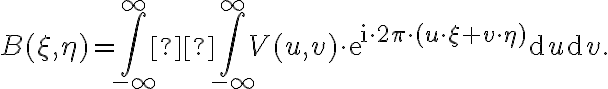
Therefore, to calculate the SNR in radio interferometry, one has to calculate the uncertainty of the brightness distribution  from the uncertainty of the complex visibility
from the uncertainty of the complex visibility  . As in every measurement, the measured data need to be sampled, meaning that the visibility is only measured at discrete locations
. As in every measurement, the measured data need to be sampled, meaning that the visibility is only measured at discrete locations 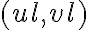 along the tracks in the
along the tracks in the 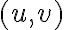 -plane. Let:
-plane. Let: 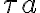 be the integration time of the individual samples in the
be the integration time of the individual samples in the 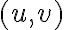 -plane,
-plane, 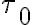 be the total integration time and
be the total integration time and 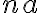 be the total number of antennas. Then the total number of measured visibilities
be the total number of antennas. Then the total number of measured visibilities 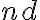 is given by
is given by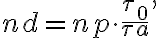
in which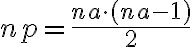
is the number of antenna pairs or rather the number of individual two-element interferometers. Since this brightness distribution suffers from incomplete 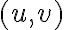 -coverage, the resulting image is called a "dirty image", which is also indicated by the superscript "D" of the brightness distribution
-coverage, the resulting image is called a "dirty image", which is also indicated by the superscript "D" of the brightness distribution 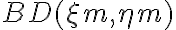 . The visibilities are measured at discrete locations
. The visibilities are measured at discrete locations 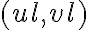 , so the brightness distribution is given by the discrete Fourier transform
, so the brightness distribution is given by the discrete Fourier transform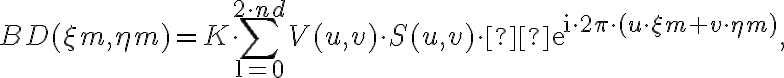
in which 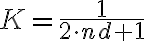 is a normalization constant and
is a normalization constant and 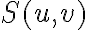 is a sampling function which is given by
is a sampling function which is given by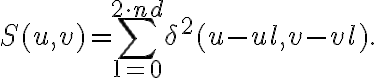
This sampling function is only non-zero where the visibility is measured in the 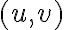 -plane.
-plane.
To suppress sidelobes, the beam shape of the observing array can be controlled by applying appropriate weights to the measured visibilities. Furthermore, if the observing array consists of telescopes that have different collecting areas 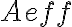 , and different receivers with different system temperatures
, and different receivers with different system temperatures 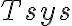 , frequency bandwidths
, frequency bandwidths 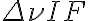 and integration times
and integration times 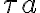 , one can also apply weights to control these differences. The weights can be written as
, one can also apply weights to control these differences. The weights can be written as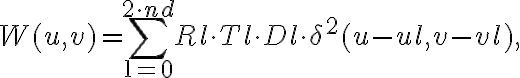
in which 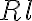 accounts for different telescope properties,
accounts for different telescope properties, 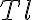 is a taper which controls the beam shape and
is a taper which controls the beam shape and 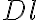 weights the density of the measured visibilities (more detailed information on the weights, especially on the
weights the density of the measured visibilities (more detailed information on the weights, especially on the 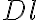 -factor, will be given in the next section 2.4.3). With these weights, the brightness distribution can then be written as
-factor, will be given in the next section 2.4.3). With these weights, the brightness distribution can then be written as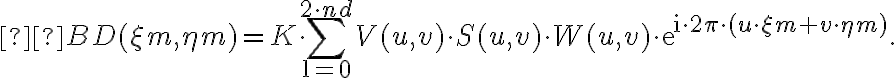
Because there is no measurement in the center of the 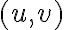 -plane, the
-plane, the 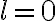 terms of the dirty image
terms of the dirty image 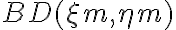 vanish, leading to
vanish, leading to![\displaystyle \begin{array}{rl} B^\text{D}(\xi_\text{m}, \eta_\text{m}) & = K \cdot \sum_{\text{l}=0}^{2\cdot n_\text{d}} V_\text{l} \cdot W_\text{l} \cdot \text{e}^{\text{i}\cdot 2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})} \\ & = 2 \cdot K \cdot \sum_{\text{l}=1}^{n_\text{d}} W_\text{l} \cdot [ \Re V_\text{l} \cdot \cos(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})) - \Im V_\text{l} \cdot \sin(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m}))] \text{,} \end{array} \displaystyle \begin{array}{rl} B^\text{D}(\xi_\text{m}, \eta_\text{m}) & = K \cdot \sum_{\text{l}=0}^{2\cdot n_\text{d}} V_\text{l} \cdot W_\text{l} \cdot \text{e}^{\text{i}\cdot 2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})} \\ & = 2 \cdot K \cdot \sum_{\text{l}=1}^{n_\text{d}} W_\text{l} \cdot [ \Re V_\text{l} \cdot \cos(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})) - \Im V_\text{l} \cdot \sin(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m}))] \text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/04c07eca8079ad16147719b4c40cf6be.gif)
in which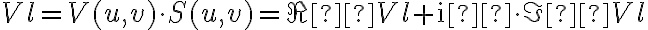
and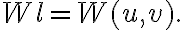
Note that the two additional terms ![\Re V_\text{l} \cdot \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \Re V_\text{l} \cdot \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/50a8ee2bb161b4b41f5ab85faa62b859.gif) and
and ![\Im V_\text{l} \cdot \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \Im V_\text{l} \cdot \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/30bd73fb80f7725027d8515833593296.gif) vanish under the integral of
vanish under the integral of 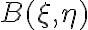 and can therefore also be neglected for the sum of
and can therefore also be neglected for the sum of 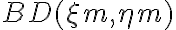 .
.
To calculate the sensitivity in the image plane, a point source at the phase and image center is considered. For such a point source, the visibility 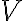 is real and constant across the entire
is real and constant across the entire 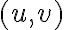 -plane and only varies due to random noise. Furthermore, because
-plane and only varies due to random noise. Furthermore, because 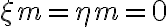 , the
, the ![\sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/9b252b33edecca4b4f2300bbdd905d3b.gif) -term vanishes and
-term vanishes and ![\cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] = 1 \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] = 1](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/423a918ff62e58d89f2ee83a7f9b4ea6.gif) . Therefore, the dirty image of such a point source is given by
. Therefore, the dirty image of such a point source is given by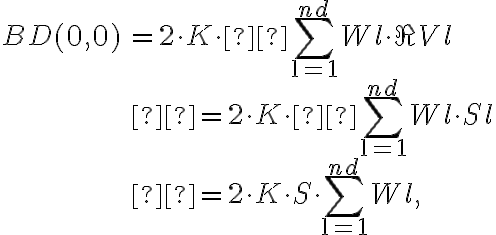
in which 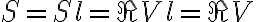 is the total flux density of the source. Note that here
is the total flux density of the source. Note that here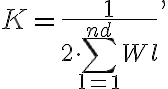
so that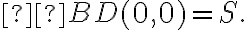
Assuming that the uncertainty of the flux density 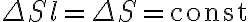 , the noise in the dirty image is given by
, the noise in the dirty image is given by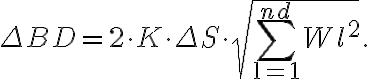
Furthermore, assuming an observing array that consists of 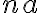 identical telescopes
identical telescopes 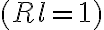 and a naturally weighted
and a naturally weighted 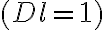 , untapered
, untapered 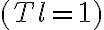 image,
image, 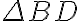 simplifies to
simplifies to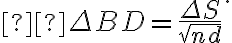
Since 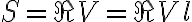 , the uncertainty of the flux density
, the uncertainty of the flux density 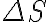 is given by the rms noise
is given by the rms noise 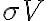 of the measured visibilities which is, based on the radiometer equation, given by
of the measured visibilities which is, based on the radiometer equation, given by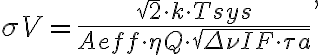
in which 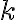 is the Boltzmann constant and
is the Boltzmann constant and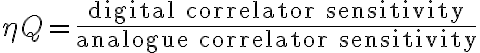
is the quantization efficiency accounting for the quantization noise due to the conversion of analogue signals to digital signals.
Inserting 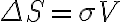 into
into 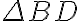 , the sensitivity for the synthesized image is finally given by
, the sensitivity for the synthesized image is finally given by