Demokurs: Introduction to Engineering Mathematics
1. Functions
1.4. Trigonometric Functions

The important characteristics of the trigonometric functions sine \((\sin)\), cosine \((\cos)\), and tangent \((\tan)\) are now to be explained.

The Basics
Trigonometric functions describe relationships between the sides and angles of a right-angled triangle. The side opposite the right angle is called hypotenuse, also identifiable as the longest side of a right triangle in Euclidean geometry. The side opposite an acute angle is called the opposite (side), and the side adjacent to it (that is not the hypotenuse) is called the adjacent (side). Note that the naming depends on which of the two acute angles is chosen. In cases where context doesn't make it obvious, one should distinguish which angle's opposite or adjacent is in question.
One obtains the graphs of these trigonometric functions by plotting the ratio of the corresponding sides (on the \(y\)-axis) against the angle \(\alpha\) in radians (on the \(x\)-axis). These are shown in the figures below.
The trigonometric functions are defined on a right-angled triangle as follows:
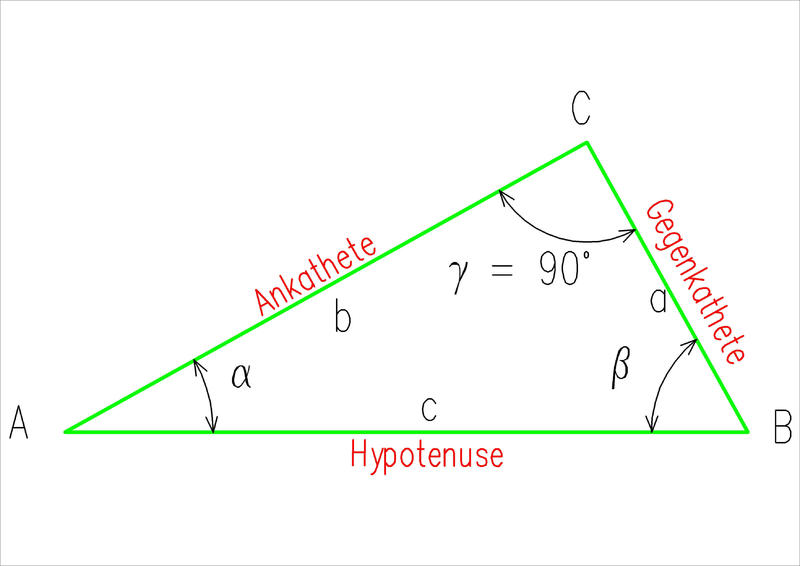
right-angled triangle
Sine
Sine is the ratio of the opposite to the hypotenuse.
Definition: Sine
\[\sin(\alpha)=\frac{\text{opposite}}{\text{hypotenuse}}\]
The term sine comes from the Latin "sinus" meaning arc or curve. Since the hypotenuse is always the longest side, the value of the sine is always smaller than 1.
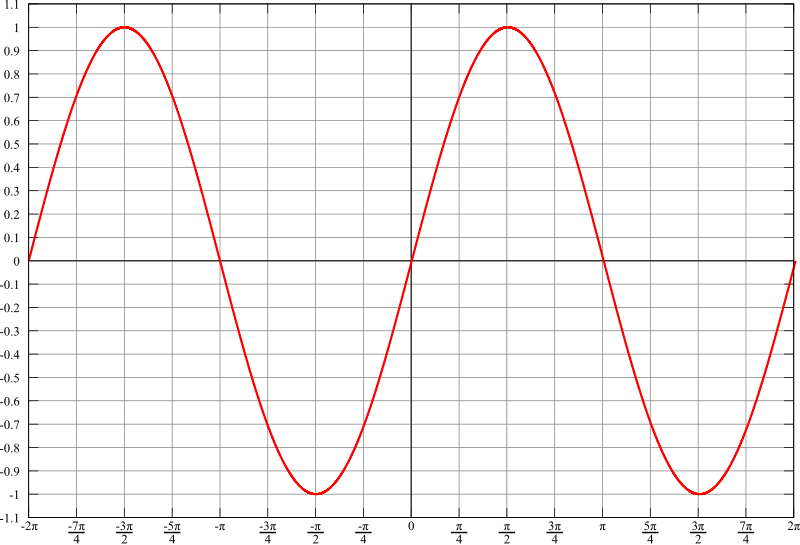
The sine function
Cosine
Cosine is the ratio of the adjacent to the hypotenuse.
Definition: Cosine
\[\cos(\alpha)=\frac{\text{adjacent}}{\text{hypotenuse}}\]
The term Cosine comes from the Latin "complementi sinus", it is the sine of the complementary angle. The value of the cosine is also obviously less than 1, because the hypotenuse is the longest side of the triangle.
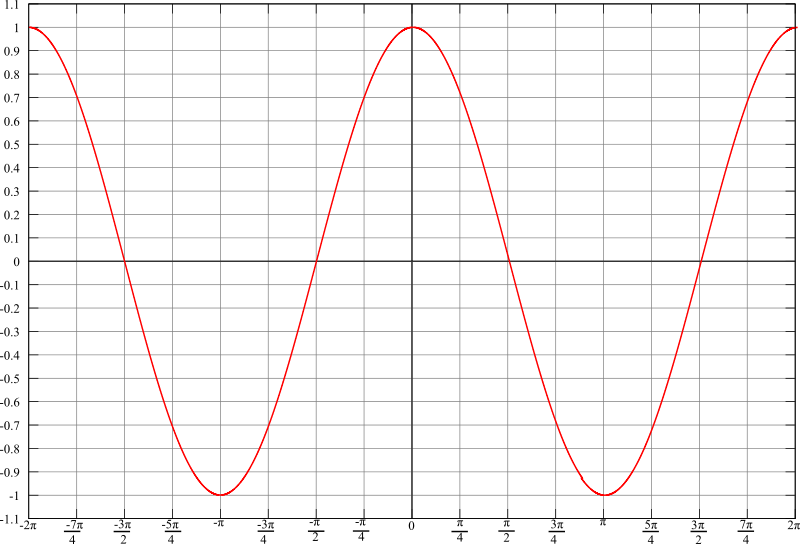
The cosine function
Tangent
Tangent is the ratio of the opposite to the adjacent.
Definition: Tangent
\[\tan(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}=\frac{\frac{\text{opposite}}{\text{hypotenuse}}}{\frac{\text{adjacent}}{\text{hypotenuse}}}=\frac{\text{opposite}}{\text{adjacent}}\]
The name tangent comes from the tangent of a unit circle. Details are in the next chapter.
The value of the tangent can easily exceed 1, because on the one hand the hypotenuse does not occur in the quotient (as it did for sine and cosine limiting their value to 1), and on the other hand the adjacent can be smaller than the opposite.
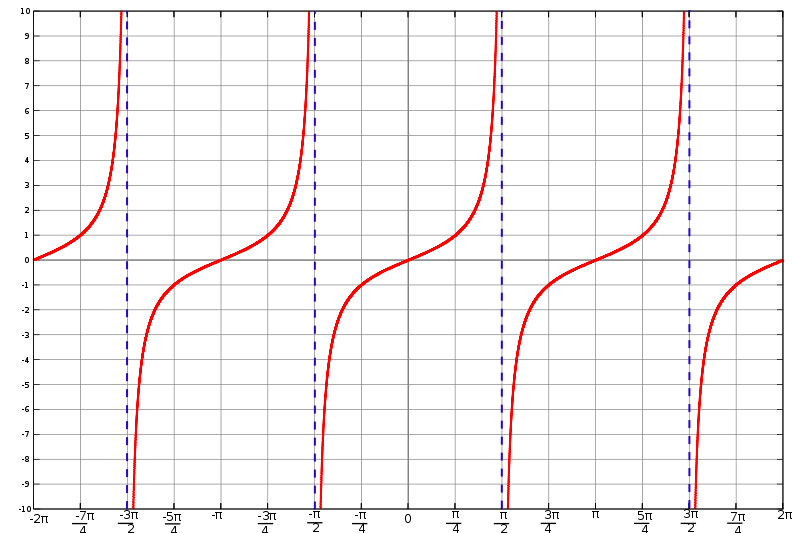
The tangent function

Trigonometry of a unit circle
If we plot a unit circle around the origin in a coordinate system and choose a point \(P\) on the unit circle in the first quadrant, we can draw a right-angled triangle in the unit circle such that the hypotenuse is the line segment connecting the origin and \(P\).
Let \(x\) be the \(x\)-coordinate and \(y\) the \(y\)-coordinate of \(P\). We can consequently determine \(\sin\), \(\cos\) and \(\tan\) using the above definitions. In this case the hypotenuse has the length 1, the values of sine and cosine are: \[\sin(\alpha)=y\qquad\quad\cos(\alpha)=x\]
With the help of Pythagorean theorem we obtain the equation \[\sin^2(\alpha)+\cos^2(\alpha)=1\]
Extend the line segment connecting the origin and \(P\) past \(P\) and draw a line tangent to the circle at the point (1,0) (this runs vertically). The tangent (tan) of the angle is equal to the length of the line segment connecting on the one hand the point of intersection between the line of origin passing through \(P\) and tangent to the circle (that runs vertically in our case) and on the other hand the point (1,0). The term tangent comes from this description.
If we choose the point \(P\) to be on the unit circle but not in the first quadrant then we obtain the values of sine, cosine and tangent for arbitrary angles.
Thereby we obtain the following relationships: \[-\sin(\alpha)=\sin(-\alpha)\qquad\quad\cos(-\alpha)=\cos(\alpha)\]
Hence sine is an odd function (the graph is point-symmetric about the origin), and cosine an even function (the graph is axially-symmetric about the \(y\)-axis). We also find that sine and cosine are periodic functions with period 360\(^{\circ}\) (\(=2\pi\)).
Tangent is likewise periodic, since \[\tan(\alpha+180^{\circ}) = \frac{\sin(\alpha+180^{\circ})}{\cos(\alpha+180^{\circ})} = \frac{-\sin(\alpha)}{-\cos(\alpha)} = \tan(\alpha)\]
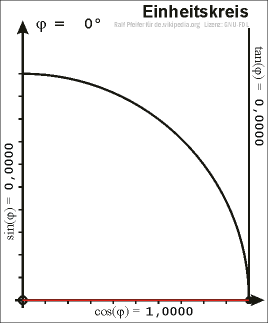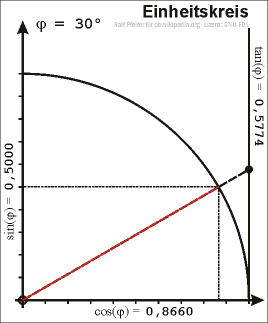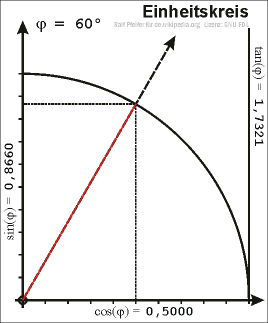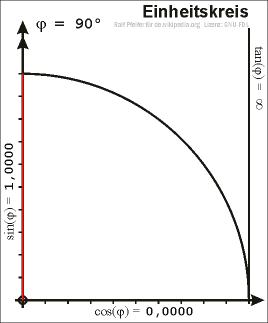
Right-angled triangle in the unit circle

General definitions of \(\text{ }\sin\), \(\text{ }\cos\text{ }\) and \(\text{ }\tan\)
More general forms of trigonometric functions \(\sin\), \(\cos\) and \(\tan\) can be given by modifying the basic functions with a number of parameters. Consider functions of the form \[a\ \cdot\ \sin(b\cdot\alpha\ -\ c)\ +\ d\] \[a\ \cdot\ \cos(b\cdot\alpha\ -\ c)\ +\ d\] \[a\ \cdot\ \tan(b\cdot\alpha\ -\ c)\ +\ d.\] Then each of the variables \(a, b, c, d\) has a distinct role, explained below.
Variation of the amplitude
The factor \(a\) changes the displacement in the \(y\)-direction:
| \(a=1\) | the normal function is given |
|---|---|
| \(a<1\) | the amplitude is lower |
| \(a>1\) | the amplitude is greater |
Change of the period
The factor \(b\) changes the period of the function:
| \(b=1\) | the normal function is given |
|---|---|
| \(b<1\) | the period repeats less frequent |
| \(b>1\) | the period repeats more frequent |
Translation in the \(x\)-direction
The factor \(c\) translates the graph in the \(x\)-direction.
| \(c=0\) | the normal function is given |
|---|---|
| \(c<0\) | displacement to the left |
| \(c>0\) | displacement to the right |
Translation in the \(y\)-direction
The factor \(d\) shifts the graph in the \(y\)-direction:
| \(d=0\) | the normal function is given |
|---|---|
| \(d<0\) | displacement downwards |
| \(d>0\) | displacement upwards |
Optional reading: Series definitions of trigonometric functions

The inverse functions of \(\text{ }\sin\), \(\text{ }\cos\text{ }\) and \(\text{ }\tan\)
The inverse functions of \(\sin\), \(\cos\) and \(\tan\) are as follows: \[\arccos: [-1,1]\ \rightarrow\ \mathbb{R}\quad\text{Arccosine}\] \[\arccos(x)\ =\ \cos^{-1}(x)\] \[\arcsin: [-1,1]\ \rightarrow\ \mathbb{R}\quad\text{Arcsine}\] \[\arcsin(x)\ =\ \sin^{-1}(x)\] \[\arctan: \mathbb{R}\ \rightarrow\ \mathbb{R}\quad\text{Arctangent}\] \[\arctan(x)\ =\ \tan^{-1}(x)\]

Some specific values of \(\text{ }\sin\), \(\text{ }\cos\text{ }\) and \(\text{ }\tan\)
| Angle | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | \(180^\circ\) | \(270^\circ\) |
|---|---|---|---|---|---|---|---|
| Radians | \(0\pi\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\pi\) | \(\frac{3\pi}{2}\) |
| Sine | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(0\) | \(-1\) |
| Cosine | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-1\) | \(0\) |
| Tangent | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | NaN | \(0\) | NaN |

New terms:
-
Sine
-
Cosine
-
Tangent
-
Trigonometry on the unit circle
-
General definition of \(\sin\), \(\cos\) and \(\tan\)
-
Inverse function of \(\sin\), \(\cos\) and \(\tan\)
Short revision exercises

Exercise 1.
Sketch the course of the functions below for \(x\in [0,2\pi]\).
-
\(\sin(2x)+3\)
-
\(\frac{\cos(x)-2}{\sin(x)+2}\)
-
\(\frac{1}{2}\cdot\tan(3x)\)

Exercise 2.
Determine the roots of the functions in exercise 1.

Exercise 3.
Given a right-angled triangle with hypotenuse of length 3 and angle \(\alpha=37^\circ\) determine the length of both sides adjacent to the right-angle.
