Schulmathematik unter didaktischen Gesichtspunkten: Stochastik in der Sekundarstufe II (Demo-Kurs)

1. Wahrscheinlichkeitsrechnung

1.5. Satz von Bayes

Satz (Totale Wahrscheinlichkeit)

Ist \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und bilden die Ereignisse \(B_1, B_2, \ldots , B_n\) von \(\Omega\) mit \(P(B_k)>0\) für alle \(k = 1, 2, \ldots , n\) eine Zerlegung von \(\Omega\), ist also:

\(B_1\cup B_2\cup \ldots\cup B_n = \Omega\) und
\(B_i\cap B_j= \emptyset\), für alle \(i\neq j,\)

dann gilt für jedes Ereignis \(A \in\wp (\Omega)\): \[P(A) = P(B_1)\cdot P(A|B_1)+P(B_2)\cdot P(A|B_2)+\ldots + P(B_n)\cdot P(A|B_n)\] \[P(A) = \sum_{k=1}^n P(B_k)\cdot P(A|B_k)\]

Für den Sonderfall \(n=2\) ergibts sich damit:

Die Ergebnismenge \(\Omega\) zerfällt nur in \(B\) und \(\overline{B}\), also \(\Omega = B\cup \overline{B}\). Für \(P(B)>0\) und \(P(\overline{B})>0\) gilt dann: \[P(A) = P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})\]

Satz (Satz von Bayes)

Es seien \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und \(A\) ein Ereignis mit \(P(A)>0\). Bilden die Ereignisse \(B_1, B_2, \ldots , B_n\) von \(\Omega\) mit \(P(B_k)>0\) für alle \(k = 1, 2, \ldots , n\) eine Zerlegung von \(\Omega\), dann gilt für jedes \(k = 1, 2, \ldots , n\): \[P(B_k|A)=\frac{P(B_k)\cdot P(A|B_k)}{P(A)} = \frac{P(B_k)\cdot P(A|B_k)}{\sum_{k=1}^n P(B_k)\cdot P(A|B_k)}\]

Für den Sonderfall \(n=2\) ergibts sich damit:

Die Ergebnismenge \(\Omega\) zerfällt nur in \(B\) und \(\overline{B}\), also \(\Omega = B\cup \overline{B}\). Für \(P(B)>0\) und \(P(\overline{B})>0\) gilt dann: \[P(B|A) = \frac{P(B)\cdot P(A|B)}{P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})} \]

Didaktische Hinweise:

Der Satz von Bayes lässt sich aus Umformungen der Definitionsgleichung der bedingten Wahrscheinlichkeit herleiten und muss deshalb im Prinzip nicht auswendig gelernt werden. Zum Beweis sei z.B. auf die Literatur verwiesen.
Für den Sonderfall \(n=2\), bei dem die Ereignismenge \(\Omega\) nur in die Ereignisse in \(B\) und \(\overline{B}\) zerfällt, lässt sich die totale Wahrscheinlichkeit \(P(A)\) für ein Ereignis \(A\) gut mittels Baumdiagramm bestimmen:
Dabei müssen die beiden bei A endenden Pfade berücksichtigt und die Multiplikations- und Additionsregeln angewendet werden: \[P(A) = P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})\]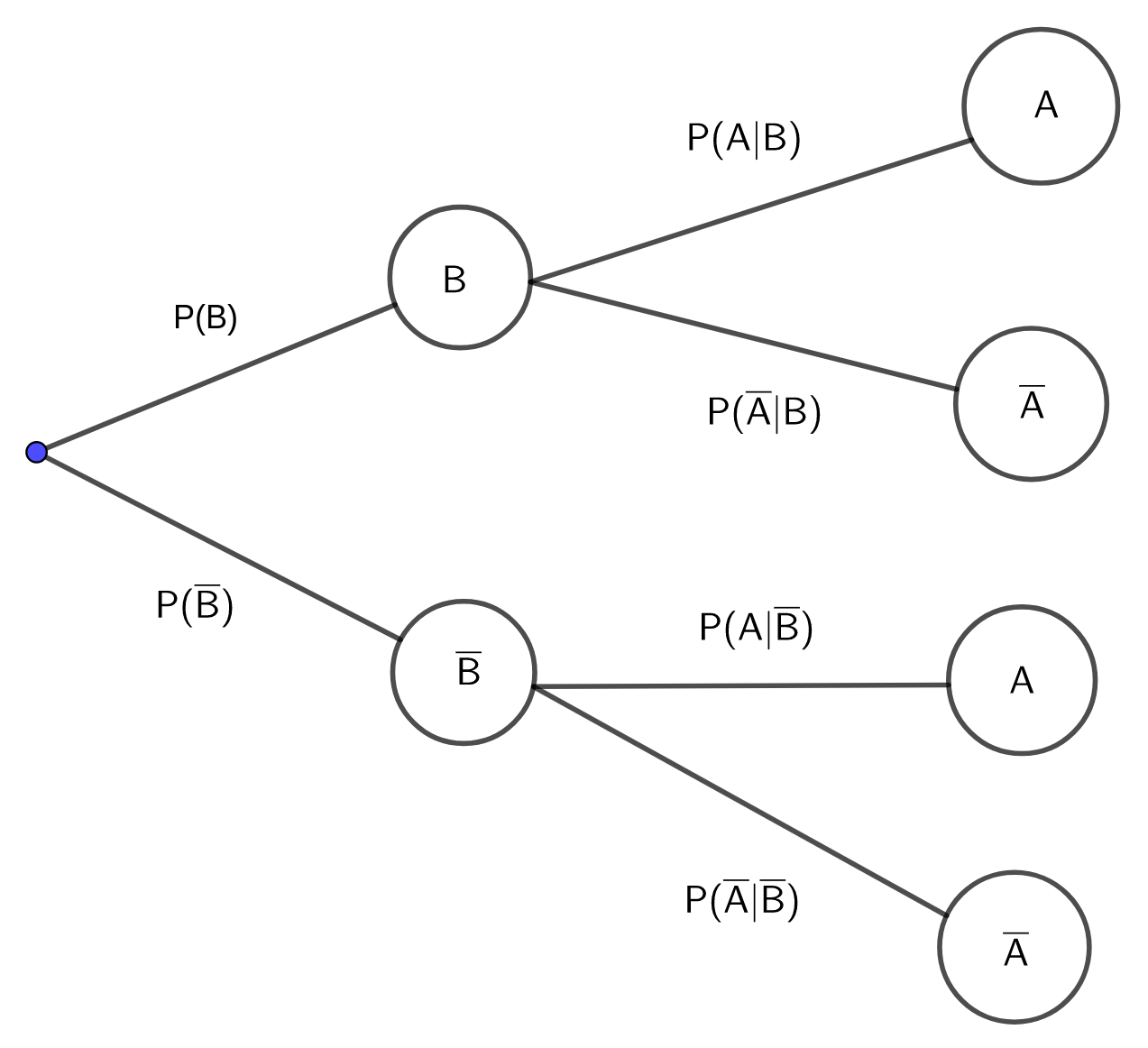
Soll die Formel von Bayes angewendet werden, wird zur Berechnung von \(P(B_k|A)\) auch Kenntnis über \(P(B_k)\) benötigt. \(P(B_k)\) wird als a-priori-Wahrscheinlichkeit für das Ereignis \(B_k\) bezeichnet, \(P(B_k|A)\) als a-posteriori-Wahrscheinlichkeit für \(B_k\).

Beispiel (Mordprozess)

Bei einem Mordprozess liegen Indizien vor, die für die Täterschaft einer bestimmten Person sprechen. Als ein solches Indiz (Ereignis \(A\) käme bspw. die „Übereinstimmung der Blutgruppe bei Blutspuren an der Kleidung der verdächtigen Person und der des Opfers“ in Frage oder die „Übereinstimmung von Textilfaserspuren an der Kleidung der verdächtigen Person und der des Opfers“.

Mit \(B\) werde das Ereignis bezeichnet, dass der Verdächtige Kontakt mit dem Opfer hatte.

Es interessiert also die Frage nach der Wahrscheinlichkeit \(P(B|A)\), dass also die verdächtige Person Kontakt mit dem Opfer hatte, unter der Bedingung, dass ein Indiz \(A\) erfüllt ist.

Mit der Formel von Bayes liegt hierfür eine Berechnungsmöglichkeit vor. Allerdings müssen dafür auch \(P(A|B)\), \(P(A)\) und \(P(B)\) bekannt sein. Gerade über letztere a-priori-Wahrscheinlichkeit \(P(B)\) ist oft wenig bekannt. Deshalb müssen Annahmen gemacht werden.

Für \(P(A|B)\) ließe sich annähernd \(1\) annehmen, denn es lässt sich mit an Sicherheit grenzender Wahrscheinlichkeit annehmen, dass sich unter der Hypothese eines Kontaktes \(B\) Indizien der zuvor beschrieben Art ergeben.

Zur Bestimmung von \(P(A)\) wird auch \(P(A|\overline{B})\) benötigt. Um diese Wahrscheinlichkeit abzuschätzen könnte man beim Indiz „Blutspuren“ die prozentuale Häufigkeit der Blutgruppe des Opfers in der Bevölkerung annehmen.

Wie sieht es allerdings mit der a-priori-Wahrscheinlichkeit \(P(B)\) („Verdächtige Person hatte Kontakt mit dem Opfer“) aus?

Eine sehr gewagte Vorgehensweise ist die eines Gutachters, der sich bei einem Mordprozess 1973/74 folgendermaßen entschied: „Ich nehme eine a-priori-Wahrscheinlichkeit von 50% für die Täterschaft des Beklagten an. Das bedeutet, dass ich ihm gegenüber unvoreingenommen bin – ich gehe davon aus, dass er ebenso schuldig wie unschuldig sein kann.“

Dieses mathematische Modell ist als unangemessen zu verwerfen! Eine solche Vorgehensweise ließe sich in einem Fall unterstützen, in dem bspw. eine von zwei Personen mit Sicherheit der Täter ist. Im Vorliegenden Fall allerdings ist die Annahme einer a-priori-Wahrscheinlichkeit von 50% für die Täterschaft unrealistisch und darf nicht verwendet werden. Eine wesentlich kleinere a-priori-Wahrscheinlichkeit wäre angemessener.

Im konkreten Mordprozess hatte der Gutachter dementsprechend eine über 90%-ige Wahrscheinlichkeit für die Täterschaft des Angeklagten errechnet. Auf Grund eines Alibis wurde dieser allerdings freigesprochen und der Prozess abgebrochen. Hieran lässt sich leicht erkennen, dass Modellannahmen leicht zu Fehlbeurteilungen führen können.

Beispiel (Medizinischer Test - "False Positives")

Ein medizinischer Test zur Früherkennung einer bestimmten Krankheit liefert bei erkrankten Personen in 96% der Fälle auch einen positiven Krankheitsbefund. Andererseits liefert dieser Test auch bei gesunden Personen in 3% der Fälle einen positiven Krankheitsbefund („falsch-positiv“).

Es wird angenommen, dass die betreffende Krankheit in der zu Grunde liegenden Population (Grundgesamtheit) bei 2% der Personen vorliegt.

Es ergeben sich also vor allem die folgenden Fragestellungen:

Wie groß ist die Wahrscheinlichkeit, dass eine zufällig „gezogene“ Person der Grundgesamtheit beim Test einen positiven Krankheitsbefund erhält?
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig aus der Gruppe der positiv getesteten Personen „gezogene“ Person tatsächlich Träger der Krankheit ist?
Wie groß ist die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit positivem Befund eigentlich gesund ist?

Wir definieren die folgenden Ereignisse:

\(K:\) "Person ist krank"
\(\overline{K}:\) "Person ist gesund"
\(T:\) "Untersuchungsbefund ist positiv"
\(\overline{T}:\) "Untersuchungsbefund ist negativ"

Unter den Modellannahmen der Aufgabe gilt: \[P(K)=0.02; P(T|K) = 0.96; P(T|\overline{K})=0.03\]

Gesucht ist die totale Wahrscheinlichkeit \(P(T)\): \[\begin{align} P(T) &= P(K)\cdot P(T|K)+P(\overline{K})\cdot P(T|\overline{K}) \\ &= 0.02\cdot 0.96 + (1-0.02)\cdot 0.03 = 0.0486 \end{align}\]
Gesucht ist die bedingte Wahrscheinlichkeit \(P(K|T)\), die sich mit der Formel von Bayes berechnen lässt: \[P(K|T) = \frac{P(K\cap T)}{P(T)} = \frac{P(K)\cdot P(T|K)}{P(T)}\] Mit a. folgt: \[P(K|T) = \frac{0.02\cdot 0.96}{0.0486} \approx 0.3951\]
Gesucht ist die bedingte Wahrscheinlichkeit \(P(\overline{K}|T)\). \[P(\overline{K}|T) = \frac{P(\overline{K})\cdot P(T|\overline{K})}{P(T)} = \frac{0.98\cdot 0.03}{0.0486} \approx 0.6049\] Die Lösung von c. lässt sich allerdings leichter bestimmen durch: \[P(\overline{K}|T) = 1 - P(K|T) = 1-0.3951 = 0.6049\]

Anmerkungen:

Die Annahme, dass die betreffende Krankheit bei 2% der Personen der Grundgesamtheit auftritt (\(P(K) = 0.02\)), geht entscheidend in alle obigen Lösungen ein – bspw. in Teil b) bei der Berechnung der a-posteriori-Wahrscheinlichkeit \(P(K|T)\).
Diese a-priori-Wahrscheinlichkeit \(P(K)\) wurde vermutlich als Schätzwert mittels relativer Häufigkeiten gefunden. Dies wirft Fragen auf: Wie groß war die untersuchte Menge an Personen? Wie homogen/inhomogen war diese? Wurden dabei Personen aus Risikogruppen berücksichtigt? Dadurch wird deutlich, dass die Lösungen im Beispiel nur Lösungen unter bestimmten Modellannahmen sind!
Mit den obigen Bezeichnungen lautet eine geeignete Ergebnismenge \(\Omega\): \[\Omega = \{(K, T), (K, \overline{T}), (\overline{K}, T), (\overline{K}, \overline{T}) \}\] Dabei bedeutet das Ereignis \(\{(\overline{K}, T), (\overline{K}, \overline{T})\}\): „Person ist gesund“

Auch bei dieser Aufgabenstellung lässt sich die Vierfeldertafel wirkungsvoll zur Unterstützung einsetzen. Das Untersuchungskollektiv ist nach zwei Merkmalen klassifiziert – Gesundheitszustand und Testergebnis. Beide Merkmale haben jeweils zwei Ausprägungen. Dies führt zu der folgenden Tabelle:

	\(K\): Person ist krank	\(\overline{K}\): Person ist gesund
\(T\): Testergebnis ist positiv	\(P(T\cap K) = 0.0192\)	\(P(T\cap \overline{K})=0.0294\)	\(P(T)=0.0486\)
\(\overline{T}\): Testergebnis ist negativ	\(P(\overline{T}\cdot K)=0.0008\)	\(P(\overline{T}\cdot \overline{K})=0.9506\)	\(P(\overline{T})=0.9514\)
	\(P(K)=0.02\)	\(P(\overline{K})=0.98\)	\(P(\Omega)=1\)

Angenommen, das Untersuchungskollektiv bestehe aus 10000 Personen. Dann ergibt sich für die im Beispiel beschriebenen Situationen die folgende absolute Verteilung:

	\(K\)	\(\overline{K}\)
\(T\)	192	294	486
\(\overline{T}\)	8	9506	9514
	200	9800	10000

Aus einer gegebenen Vierfeldertafel lassen sich zwei verschiedene Baumdiagramme gewinnen – abhängig davon, ob \(\Omega\) zuerst nach dem einen Merkmal zerlegt wird oder zuerst nach dem anderen. Seien bspw. die Zerlegungen von \(\Omega\) einerseits männlich (M) und weiblich (W) und andererseits krank (K) und gesund (\(\overline{K}\)). Dann ergeben sich die beiden folgenden Baumdiagramme, deren Pfade sich jeweils im entsprechenden Feld der Vierfeldertafel „treffen“:
Im Baumdiagramm lassen sich die bedingten Wahrscheinlichkeiten unmittelbar ablesen. In der Vierfeldertafel hingegen müssen sie aus deren Daten erst berechnet werden.
Die Stufung im Baumdiagramm legt eine Orientierung, bzw. Richtung in der Reihenfolge der Ereignisse fest. Dieser dynamische Charakter des Diagramms (im Gegensatz zum statischen Charakter der Vierfeldertafel) kann die Lösung einer Aufgabe unter Umständen erschweren. Bspw. kann im linken obigen Diagramm die bedingte Wahrscheinlichkeit P(W|K) abgelesen werden, aber nicht die bedingte Wahrscheinlichkeit P(K|W).