Grundlagen
Die trigonometrsichen Funktionen beschreiben Zusammenhänge zwischen den Seiten und Winkeln eines rechtwinkligen Dreiecks. Als Hypotenuse bezeichnet man die dem rechten Winkel gegenüber liegende Seite des Dreiecks. Die Gegenkathete ist die Seite des Dreiecks, die dem Winkel gegenüber liegt, der gerade betrachtet wird. Die Ankathete ist die direkt am Winkel anliegende Seite (die nicht die Hypotenuse ist).
Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik
1. Funktionen
1.4. Trigonometrische Funktionen


Die Trigonometrischen Funktionen Sinus, Cosinus, und Tangens
Nun sollen die wichtigsten Eigenschaften der trigonometrischen Funktionen (oft auch Winkelfunktionen genannt) Sinus (\(\sin\)), Cosinus (\(\cos\)) und Tangens (\(\tan\)) erläutert werden.
Nun sollen die wichtigsten Eigenschaften der trigonometrischen Funktionen (oft auch Winkelfunktionen genannt) Sinus (\(\sin\)), Cosinus (\(\cos\)) und Tangens (\(\tan\)) erläutert werden.
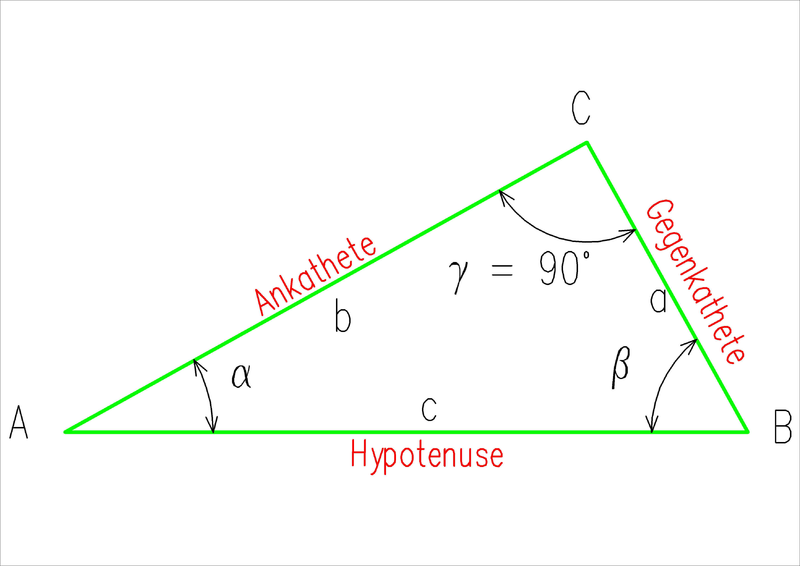 rechtwinkliges Dreieck
rechtwinkliges DreieckTrägt man das Verhältnis der entsprechenden Seiten in Abhängigkeit des Winkels \(\alpha\) in ein Koordinatensystem (\( \alpha = x\) auf der x-Achse) im Bogenmaß ein, so erhält man die in den Zeichnungen abgebildeten Funktionsgraphen.
Die Trigonometrischen Funktionen sind am rechtwinkeligen Dreieck wie folgt definiert:
Sinus
Der Sinus ist das Verhältnis der Längen von Gegenkathete und Hypotenuse.
Die Trigonometrischen Funktionen sind am rechtwinkeligen Dreieck wie folgt definiert:
Sinus
Der Sinus ist das Verhältnis der Längen von Gegenkathete und Hypotenuse.

Definition (Sinus)
\(\sin(\alpha) = \frac {Gegenkathete}{Hypotenuse}\)
\(\sin(\alpha) = \frac {Gegenkathete}{Hypotenuse}\)
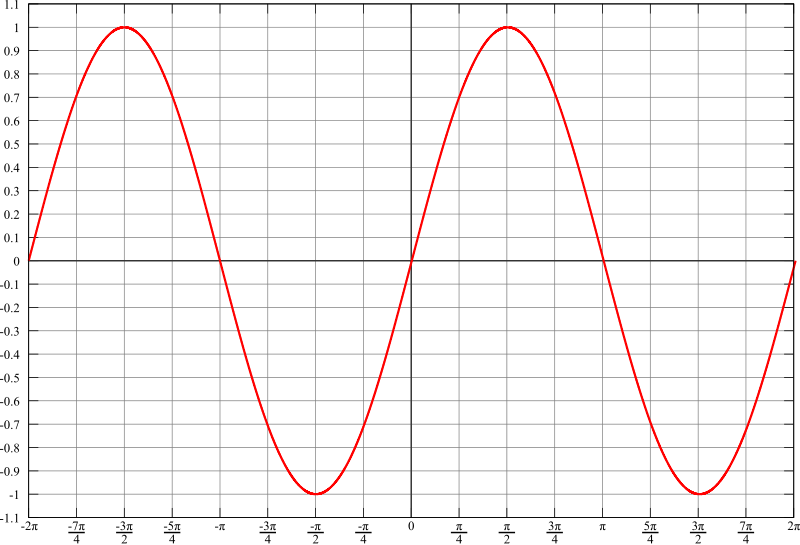 Sinusfunktion
SinusfunktionDer Begriff Sinus stammt aus dem Lateinischen für Bogen, Krümmung.
Da in der Geometrie die Hypotenuse immer die längste Seite im Dreieck ist, ist der Wert des Sinus immer kleiner \(1\).
Cosinus
Der Cosinus ist das Verhältnis der Längen von zwischen Ankathete und Hypotenuse.
Der Cosinus ist das Verhältnis der Längen von zwischen Ankathete und Hypotenuse.

Definition (Cosinus)
\(\cos(\alpha) = \frac {Ankathete}{Hypotenuse}\)
\(\cos(\alpha) = \frac {Ankathete}{Hypotenuse}\)
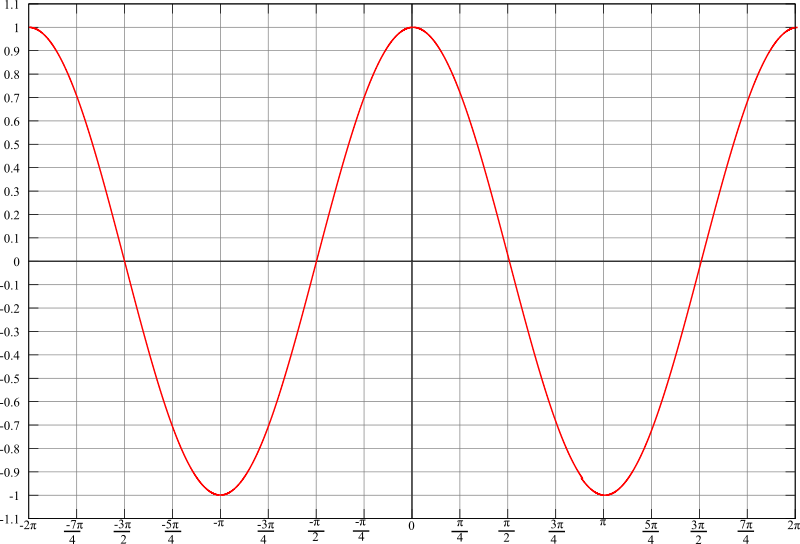 Cosinusfunktion
CosinusfunktionDie Bezeichnung Cosinus ergibt sich aus complementi sinus, also dem Sinus des Komplementärwinkels.
Für den Cosinus gilt natürlich auch, dass der Wert immer kleiner \(1\) ist, da die Hypotenuse die längste Seite ist.
Tangens
Der Tangens ist das Verhältnis der Längen von Gegenkathete zu Ankathete.
Der Tangens ist das Verhältnis der Längen von Gegenkathete zu Ankathete.

Definition (Tangens)
\(\tan(\alpha) = \frac {\sin(\alpha)}{\cos(\alpha)} = \frac{\frac{Gegenkathete}{Hypotenuse}}{\frac{Ankathete}{Hypotenuse}} = \frac{Gegenkathete}{Ankathete}\)
\(\tan(\alpha) = \frac {\sin(\alpha)}{\cos(\alpha)} = \frac{\frac{Gegenkathete}{Hypotenuse}}{\frac{Ankathete}{Hypotenuse}} = \frac{Gegenkathete}{Ankathete}\)
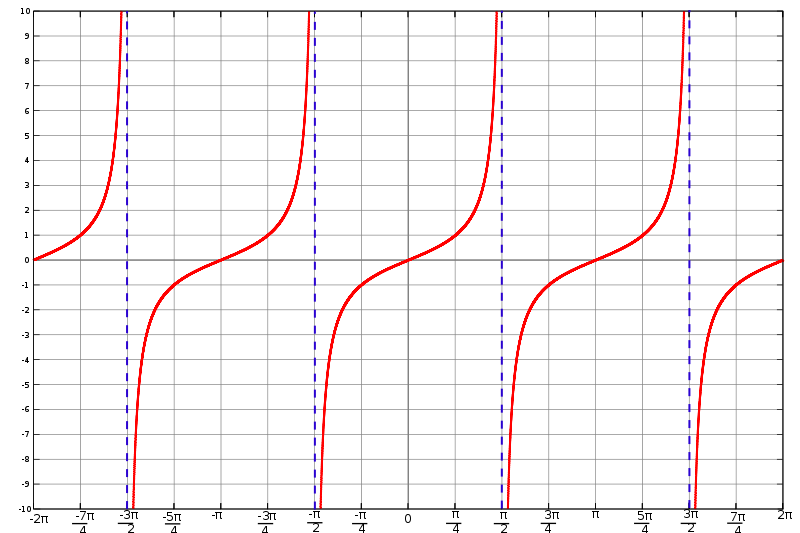 Tangensfunktion
TangensfunktionDer Name Tangens lässt sich aus der Definition des Tangens am Einheitskreis ableiten. Näheres dazu im nächsten Kapitel.
Der Wert des Tangens kann \(1\) leicht überschreiten, da zum einen im Verhältnis die Hypotenuse nicht mehr vorkommt (was beim Sinus und Cosinus der Grund für die Wertgrenze war), und zum anderen die Ankathete durchaus kleiner sein kann als die Gegenkathete.
Trigonometrie am Einheitskreis
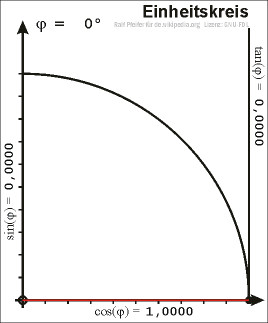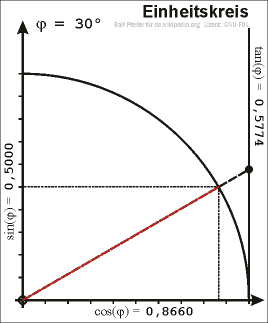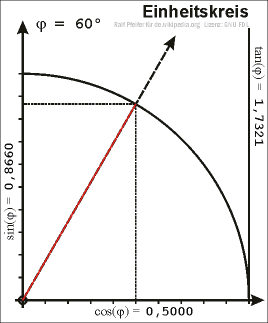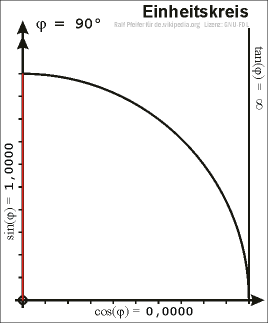
Zeichnet man in einem Koordinatensystem den Einheitskreis um den Ursprung (Nullpunkt) und wählt im ersten Quadranten einen Punkt \(P\) auf dem Einheitskreis, so kann man ein rechtwinkliges Dreieck in den Einheitskreis dermaßen einzeichnen, dass die Strecke vom Nullpunkt zu \(P\) als Hypotenuse anzusehen ist.
\(x\) ist dann also die x-Koordinate von \(P\) und \(y\) die y-Koordinate.
Somit kann man \(\sin\), \(\cos\) und \(\tan\) wieder mittels der obigen Definitionen bestimmen. Da die Hypotenuse in diesem Fall genau die Länge \(1\) hat, ergeben sich für den Sinus und Cosinus die Werte
\(\sin(\alpha) = y\) und \(\cos(\alpha) = x\)
Mit Hilfe des Satzes von Pythagoras erhält man die Gleichung
\(\sin^2(\alpha) + \cos^2(\alpha) = 1\)
Verlängert man die Strecke \(\overline{0P}\) über \(P\) hinaus und zeichnet im Punkt \((1,0)\) eine Tangente an den Einheitskreis (diese verläuft dann senkrecht), so entspricht der Tangens der Strecke zwischen dem Punkt \((1,0)\) und dem Schnittpunkt der Urspungsgeraden durch \(P\) und der Tangente. Aus dieser Beziehung folgt auch der Name Tangens. Wählt man den Punkt \(P\) auf dem Einheitskreis aber außerhalb des ersten Quadranten, so ergeben sich für den Sinus, Cosinus und Tangens auch die Werte für beliebige Winkel.
Dabei lassen sich folgende Beziehungen erkennen:
\(-\sin(\alpha) = \sin(-\alpha)\)
\(cos(-\alpha) = \cos (\alpha)\)
Der Sinus ist also eine ungerade (der Graph ist punktsymmetrisch zum Ursprung) Funktion, der Cosinus eine gerade (der Graph ist achsensymmetrsich zur y-Achse) Funktion.
Man erkennt auch, dass Sinus und Cosinus periodische Funktionen sind mit der Periode \(360°(= 2\pi)\).
Der Tangens ist ebenfalls periodisch, da gilt:
\(\tan(\alpha + 180°) = \frac{\sin(\alpha + 180°)}{\cos(\alpha + 180°)} = \frac{-\sin(\alpha)}{-\cos(\alpha)} = \tan(\alpha)\)
Zeichnet man in einem Koordinatensystem den Einheitskreis um den Ursprung (Nullpunkt) und wählt im ersten Quadranten einen Punkt \(P\) auf dem Einheitskreis, so kann man ein rechtwinkliges Dreieck in den Einheitskreis dermaßen einzeichnen, dass die Strecke vom Nullpunkt zu \(P\) als Hypotenuse anzusehen ist.
\(x\) ist dann also die x-Koordinate von \(P\) und \(y\) die y-Koordinate.
Somit kann man \(\sin\), \(\cos\) und \(\tan\) wieder mittels der obigen Definitionen bestimmen. Da die Hypotenuse in diesem Fall genau die Länge \(1\) hat, ergeben sich für den Sinus und Cosinus die Werte
\(\sin(\alpha) = y\) und \(\cos(\alpha) = x\)
Mit Hilfe des Satzes von Pythagoras erhält man die Gleichung
\(\sin^2(\alpha) + \cos^2(\alpha) = 1\)
Verlängert man die Strecke \(\overline{0P}\) über \(P\) hinaus und zeichnet im Punkt \((1,0)\) eine Tangente an den Einheitskreis (diese verläuft dann senkrecht), so entspricht der Tangens der Strecke zwischen dem Punkt \((1,0)\) und dem Schnittpunkt der Urspungsgeraden durch \(P\) und der Tangente. Aus dieser Beziehung folgt auch der Name Tangens. Wählt man den Punkt \(P\) auf dem Einheitskreis aber außerhalb des ersten Quadranten, so ergeben sich für den Sinus, Cosinus und Tangens auch die Werte für beliebige Winkel.
Dabei lassen sich folgende Beziehungen erkennen:
\(-\sin(\alpha) = \sin(-\alpha)\)
\(cos(-\alpha) = \cos (\alpha)\)
Der Sinus ist also eine ungerade (der Graph ist punktsymmetrisch zum Ursprung) Funktion, der Cosinus eine gerade (der Graph ist achsensymmetrsich zur y-Achse) Funktion.
Man erkennt auch, dass Sinus und Cosinus periodische Funktionen sind mit der Periode \(360°(= 2\pi)\).
Der Tangens ist ebenfalls periodisch, da gilt:
\(\tan(\alpha + 180°) = \frac{\sin(\alpha + 180°)}{\cos(\alpha + 180°)} = \frac{-\sin(\alpha)}{-\cos(\alpha)} = \tan(\alpha)\)
 rechtwinkliges Dreieck im Einheitskreis
rechtwinkliges Dreieck im EinheitskreisAllgemeine Definition von \(\sin\), \(\cos\) und \(\tan\)
Die allgemeine Form der Trigonometrischen Funktionen \(\sin\), \(\cos\) und \(\tan\) kann man folgendermaßen angeben:
\(\sin(\alpha) = a \cdot \sin(b \cdot \alpha - c) + d\)
\(\cos(\alpha) = a \cdot \cos(b \cdot \alpha - c) + d\)
\(\tan(\alpha) = a \cdot \tan(b \cdot \alpha - c) + d\)
Die allgemeine Form der Trigonometrischen Funktionen \(\sin\), \(\cos\) und \(\tan\) kann man folgendermaßen angeben:
\(\sin(\alpha) = a \cdot \sin(b \cdot \alpha - c) + d\)
\(\cos(\alpha) = a \cdot \cos(b \cdot \alpha - c) + d\)
\(\tan(\alpha) = a \cdot \tan(b \cdot \alpha - c) + d\)
Veränderung der Amplitude
Der Faktor \(a\) verändert hier die Auslenkung in y-Richtung. Es gilt:
Der Faktor \(a\) verändert hier die Auslenkung in y-Richtung. Es gilt:
| \(a = 1\) | die "normale" Funktion wird angegeben |
| \(a<1\) | die Amplitude ist schwächer |
| \(a>1\) | die Amplitude ist stärker |
Änderung der Periode
Der Faktor \(b\) verändert die Periode der Funktion. Es gilt:
Der Faktor \(b\) verändert die Periode der Funktion. Es gilt:
| \(b = 1\) | die "normale" Funktion wird angegeben |
| \(b<1\) | die Periode wird seltener |
| \(b>1\) | die Periode wird häufiger |
Verschiebung in x-Richtung
Der Faktor \(c\) verschiebt den Graph der Funktion in x-Richtung. Es gilt:
Der Faktor \(c\) verschiebt den Graph der Funktion in x-Richtung. Es gilt:
| \(c = 0\) | die "normale" Funktion wird angegeben |
| \(c<0\) | Verschiebung nach links |
| \(c>0\) | Verschiebung nach rechts |
Verschiebung in y-Richtung
Der Faktor \(d\) verschiebt den Graph der Funktion in y-Richtung. Es gilt:
Der Faktor \(d\) verschiebt den Graph der Funktion in y-Richtung. Es gilt:
| \(d = 0\) | die "normale" Funktion wird angegeben |
| \(d<0\) | Verschiebung nach unten |
| \(d>0\) | Verschiebung nach oben |
Nebenbemerkung (freiwillig):

Satz 1 (Reihendarstellung von \(\cos\) und \(\sin\)):
Für alle \(x \in \mathbb{R}\) gilt:
\(\cos(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k}}{(2k)!}}\)
\(\sin(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k+1}}{(2k+1)!}}\)
Für alle \(x \in \mathbb{R}\) gilt:
\(\cos(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k}}{(2k)!}}\)
\(\sin(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k+1}}{(2k+1)!}}\)

Umkehrfunktionen von \(\sin\), \(\cos\) und \(\tan\)
Die Umkehrfunktionen von \(\sin\), \(\cos\) und \(\tan\) lauten wie folgt:
Arcuscosinus: \(\arccos: [-1, 1] \rightarrow \mathbb{R}\)
\(\arccos(x) = \cos^{-1}(x)\)
Arcussinus: \(\arcsin: [-1, 1] \rightarrow \mathbb{R}\)
\(\arcsin(x) = \sin^{-1}(x)\)
Arcustangens: \(\arctan: \mathbb{R} \rightarrow \mathbb{R}\)
\(\arctan(x) = \tan^{-1}(x)\)
Die Umkehrfunktionen von \(\sin\), \(\cos\) und \(\tan\) lauten wie folgt:
Arcuscosinus: \(\arccos: [-1, 1] \rightarrow \mathbb{R}\)
\(\arccos(x) = \cos^{-1}(x)\)
Arcussinus: \(\arcsin: [-1, 1] \rightarrow \mathbb{R}\)
\(\arcsin(x) = \sin^{-1}(x)\)
Arcustangens: \(\arctan: \mathbb{R} \rightarrow \mathbb{R}\)
\(\arctan(x) = \tan^{-1}(x)\)
Einige besondere Werte von \(\sin\), \(\cos\) und \(\tan\)
| Winkel | \(0°\) | \(30°\) | \(45°\) | \(60°\) | \(90°\) | \(180°\) | \(270°\) |
| Bogenmaß | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\pi\) | \(\frac{3 \pi}{2}\) |
| Sinus | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(0\) | \(-1\) |
| Cosinus | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-1\) | \(0\) |
| Tangens | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | Pol | \(0\) | Pol |

Aufgabe 1:
Skizzieren Sie den Verlauf der Graphen der Funktionen für \(x \in [0, 2\pi]\).
Aufgabe 2:
Bestimmen Sie die Nullstellen der in Aufgabe 1 genannten Funktionen.
Aufgabe 3:
Gegeben sei ein rechtwinkliges Dreieck mit der Hypotenusenlänge \(3\) und dem Winkel \(\alpha = 37°\). Bestimmen Sie die Länge der beiden Katheten.
Skizzieren Sie den Verlauf der Graphen der Funktionen für \(x \in [0, 2\pi]\).
- \(\sin(2x) + 3\)
- \(\frac{\cos(x) - 2}{\sin(x)+2}\)
- \(\frac{1}{2} \cdot \tan(3x)\)
Aufgabe 2:
Bestimmen Sie die Nullstellen der in Aufgabe 1 genannten Funktionen.
Aufgabe 3:
Gegeben sei ein rechtwinkliges Dreieck mit der Hypotenusenlänge \(3\) und dem Winkel \(\alpha = 37°\). Bestimmen Sie die Länge der beiden Katheten.
