Potenzfunktionen, Polynome und Potenzreihen
In diesem Kapitel wiederholen wir zunächst die Eigenschaften von Potenzfunktionen und Polynomen. In einem freiwilligen Exkurs führen wir dann noch ein wichtiges Konzept der Analysis ein - die Potenzreihen.
Potenzfunktionen

Definition 1 (Potenzfunktion mit natürlichem Exponenten)
Eine Potenzfunktion mit natürlichem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^n\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}\)
\(n=1,2,3,\cdots \)
Zwei Spezialfälle einer Potenzfunktion sind uns bereits aus dem letzten Kapitel bekannt:
Für \(n=1\) ergibt sich die reine lineare Funktion \(f\) mit \(f(x) = ax\) un für \(n=2\) ergibt sich die reine quadratische Funktion \(f\) mit \(f(x) = ax^2\).
Außerdem ergibt sich für \(n=0\) der Spezialfall einer konstanten Funktion \(f(x) = a∙x^0 = a∙1 = a\).

Aufgabe: Variieren Sie bei folgendem Beispiel für
\(f(x) = a \cdot x^3\) den Parameter
\(a\). Erläutern Sie die Veränderung des Graphen.

Definition 2 (Potenzfunktion mit ganzzahligem Exponenten)
Eine Potenzfunktion mit ganzzahligem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^z\) mit \(a \in \mathbb{R}, z \in \mathbb{Z}, D = \mathbb{R}\backslash\{0\}\)
\(z=\cdots ,-2,-1,0,1,2,\cdots \)
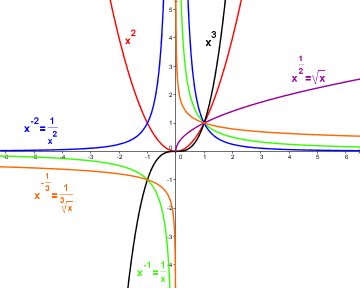
Die Potenzfunktionen mit ganzzahligem Exponenten lassen sich in zwei Gruppen mit gegensätzlichen Eigenschaften teilen:
\(f(x) = a \cdot x^n\) (natürlicher Exponent, \(n>0\)):
Diese Funktionen haben eine Nullstelle bei \(x = 0\) und divergieren für große \(|x|\) (dh. sie gehen gegen plus unendlich oder minus unendlich). Sie sind auf ganz \(\mathbb{R}\) stetig. Ihre Graphen nennt man Parabeln \(n\)-ter Ordnung.
\(f(x) = a \cdot x^{-n}\) (negativer natürlicher Exponent, \(-n<0\)):
Diese Funktionen haben eine Polstelle bei \(x = 0\) und konvergieren für große \(|x|\) gegen \(0\). Sie sind auf \(\mathbb{R}\backslash\{0\}\) stetig. Ihre Graphen nennt man Hyperbeln n-ter Ordnung. Sie haben auf Grund der Polstelle zwei Äste.
Die Graphen von Potenzfunktionen mit ungeradem Exponent sind punktsymmetrisch zum Ursprung, die von Potenzfunktionen mit geradem Exponent sind achsensymmetrisch zur y-Achse.
\(f(-x) = (-x)^2 = x^2 = f(x)\)
\(f(-x) = (-x)^3 = -(x^3) = -f(x)\)
Für wachsende \(x\) wird der Betrag von \(x^n\) immer größer und divergiert deshalb gegen \(\infty\)

Definition 3 (Potenzfunktion mit Stammbruch im Exponenten)
Eine Potenzfunktion mit Stammbruch im Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{\frac{1}{n}}\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}_0^+\)

Aufgabe: Unten sehen Sie den Graphen der Funktion
\(f\) mit
\(f(x) = x^{\frac{1}{n}}\) für
\(n \in \{2, 3, 4, 5, 6\}\). Beschreiben Sie den Graphen und achten Sie dabei auf Definitionsbereich, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründen Sie!
Beispiel 1 (Wurzelfunktion):
Insbesondere ist die Funktion
\(f: \mathbb{R}_0^+ \rightarrow \mathbb{R}_0^+, x \rightarrow \sqrt{x} = x^{\frac{1}{2}}\),
die jeder positiven Zahl ihre Quadratwurzel zuordnet, eine Potenzfunktion. Analog sind auch die k-ten Wurzeln \( \sqrt[k]{x}\) Potenzfunktionen vermöge der Festlegung \(\sqrt[k]{x} = x^{\frac{1}{k}}\). Die k-te Wurzelfunktion \(f\) mit \(f(x) = x^{\frac{1}{k}} \) ist die Umkehrfunktion zur Potenzfunktion \(g\) mit \(g(x) = x^k\) und \(g\) ist die Umkehrfunktion zu \(f\).

Definition 4 (Potenzfunktion mit negativem Stammbruch im Exponenten)
Eine Potenzfunktion mit negativem Stammbruch im Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{ - \frac{1}{n}}\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}^+\)

Aufgabe: Vergleichen Sie die Graphen der Funktionen mit negativen Stammbrüchen im Exponenten (blau) mit den bereits bekannten Graphen der Funktionen mit poitiven Stammbrüchen im Exponenten (rot gestrichelt). Achten Sie dabei auf Definitionsbereich, Symmetrie, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründen Sie.

Definition 5 (Potenzfunktion mit rationalem Exponenten)
Eine Potenzfunktion mit rationalem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{\frac{p}{q}}\) mit \(a \in \mathbb{R}, p \in \mathbb{Z}, q \in \mathbb{N}, D = \mathbb{R}^+\)

Aufgabe: Vergleichen Sie den Graphen der Potenzfunktionen mit rationalem Exponenten (blau) mit dem, den Sie schon aus den obigen Abschnitten kennen (rot und lila gestrichelt); mit dem Schieberegler können Sie dazu wieder die Exponenten verändern. Beschreiben Sie Gemeinsamkeiten und Unterschiede der Graphen! Achten Sie dabei auf Definitionsbereich und Symmetrie.
Die Darstellung von Funktionen der Form \(f(x) = (\sqrt[k]{x})^p\) als \(f(x) = x^{\frac{p}{k}}\) spielt vor allem beim Ableiten von Funktionen eine Rolle, da sich die bekannten Ableitungsregeln damit auch auf Wurzel-Funktionen übertragen lassen.
Polynome
Polynome werden aus den Potenzfunktionen \(ax^n\) mit natürlichem \(n\) mittels Addition gebildet. Sie sind auf ganz \(\mathbb{R}\) definiert und stetig.

Definition 6 (Polynom vom Grad n)
Zu \(a_0, a_1, \ldots, a_n \in \mathbb{R}\) heißt
\(p: \mathbb{R} \rightarrow \mathbb{R}, x \rightarrow \sum_{k=0}^n {a_k x^k} = a_0 + a_1 x + a_2 x^2 + \ldots + a_n x^n\)
Polynom vom Grad \(n\), falls \(a_n \ne 0\).
Nach Definition sind also konstante, lineare, quadratische und Potenzfunktionen Polynome.
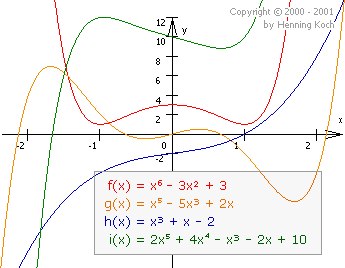
Die Graphen der Polynome mit Grad \(>2\) besitzen ein nicht mehr so leicht bestimmbares Verhalten und Aussehen wie die Spezialfälle der Graphen konstanter, linearer und quadratischer Funktionen. Um die Eigenschaften dieser Polynome und deren Graphen zu bestimmen, wendet man das aus der Schule bekannte Verfahren der Kurvendiskussion an (siehe rechts).
Polynome bei denen nur gerade Exponenten auftreten sind achsensymmetrisch zur y-Achse, Polynome bei denen nur ungerade Exponenten auftreten sind punktsymmetrisch zum Ursprung.
Polynome sind in der Analysis von großer Bedeutung, da sie eine (relativ) einfache Funktionenklasse darstellen. Insbesondere sind sie leicht zu differenzieren und integrieren. Darüber hinaus gibt es viele Möglichkeiten komplizierte Funktionen durch Polynome anzunähern.
Exkurs: Potenzreihen (freiwillig)
Betrachtet man nun unendliche Summen von Potenzfunktionen, so erhält man "Potenzreihen".

Definition 7 (Potenzreihe)
Sei \((a_n)_n\) eine Folge reeller Zahlen und \(x,a \in \mathbb{R}\). Dann heißt die Reihe
\(\sum_{n=0}^\infty {a_n (x-a)^n}\)
Potenzreihe mit Koeffizienten \(a_n\) und Entwicklungspunkt \(a\).
Polynome sind also ein Spezialfall von Potenzreihen, bei denen unendlich viele Koeffizienten \(0\) sind.
Potenzreihen stellen ein mächtiges Werkzeug in der Analysis dar. Im folgenden geben wir zwei Beispiele für Potenzreihen. Ausführlich werden diese in der Analysisvorlesung zu Studienbeginn behandelt.
Beispiel 2 (geometische Reihe):
Die geometrische Reihe
\(\sum_{n=0}^\infty {x^n}\)
konvergiert für alle \(x \in (-1; 1)\). Hier stellt sie die Funktion \(f\) mit
\(f (x) = \frac{1}{1-x}\)
dar.

Aufgabe:
Zeigen Sie dies, indem Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Glieder berechnen.
Beispiel 3 (Exponentialreihe):
Die Funktion \(f\) mit
\(f(x) = \sum_{n=0}^\infty {\frac{1}{n!} x^n}\)
ist auf ganz \(\mathbb{R}\) definiert. Mehr zu dieser speziellen Funktion lernen wir im nächsten Kapitel...

Aufgabe:
Berechnen Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Reihenglieder.

Aufgaben:
- Skizzieren Sie den Verlauf folgender Potenzfunktionen: \(x^3\), \(x^{\frac{1}{3}}\), \(x^{-3}\), \(x^{- \frac{1}{3}}\)
- Geben Sie für die Polynomfunktion mit \(f(x) = - \frac{1}{4} x^4 + \frac{3}{2} x^2 - 2x -2\) Art und Lage der Extrempunkte, die Wendepunkte und die Nullstellen an.